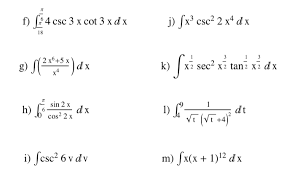By Study Rhino
Algebra is often considered a turning point in a student’s mathematical journey. It marks the shift from arithmetic — where numbers and operations dominate — to a world where letters, symbols, and abstract reasoning become just as important. While algebra can seem intimidating at first, understanding its basic concepts lays a strong foundation for success in higher-level math and real-life problem-solving.
In this comprehensive guide, we’ll explore the basic concepts of algebra, provide examples, and explain why learning algebra is important for students of all ages.
What is Algebra?
At its core, algebra is a branch of mathematics that uses symbols, usually letters, to represent numbers in formulas and equations. These symbols allow us to generalize mathematical relationships and solve problems where some values are unknown.
For example:
If you know that x + 3 = 7, you can find the value of x by subtracting 3 from both sides.
So, x = 4.
In this equation, x is a variable — a symbol that stands in for an unknown value. Algebra is the tool we use to find what that value is.
Why is Algebra Important?
Many students ask, “When will I ever use this in real life?” The truth is, algebra is more useful than it may first appear. Here’s why:
- Problem-Solving: Algebra teaches logical thinking and step-by-step problem-solving — skills useful in any career.
- Everyday Situations: From calculating expenses and budgeting to adjusting recipes or comparing mobile data plans, algebra is part of daily decision-making.
- Foundation for Higher Math: Algebra is the foundation for geometry, trigonometry, calculus, and beyond.
- Careers and Technology: Professions in science, engineering, technology, data analysis, finance, and medicine rely heavily on algebraic thinking.
Key Vocabulary in Algebra
Before we dive deeper, let’s understand some common terms used in algebra:
| Term | Definition |
| Variable | A letter (like x or y) that represents an unknown value. |
| Constant | A fixed value that doesn’t change. |
| Coefficient | A number multiplied by a variable (e.g., 5 in 5x). |
| Expression | A combination of variables, constants, and operations (e.g., 3x + 2). |
| Equation | A statement where two expressions are equal (e.g., 2x + 1 = 7). |
| Term | A part of an expression separated by + or – signs (e.g., in 4x + 3, both are terms). |
| Operator | Symbols like +, −, ×, and ÷ used in expressions. |
Basic Algebraic Concepts
Let’s break down some essential algebraic ideas in an easy-to-understand way.
- Variables and Expressions
As mentioned, a variable is a letter used to represent an unknown number. When combined with numbers and operations, it forms an algebraic expression.
Example:
If we say, “A number plus 5,” we write:
x + 5
Here, x is the unknown number (variable), and the entire statement is an algebraic expression.
- Simplifying Expressions
Just like you simplify numbers (e.g., 4 + 6 = 10), you can simplify algebraic expressions by combining like terms.
Like terms are terms that have the same variable raised to the same power.
Example:
Simplify: 3x + 5x
Since both terms have the same variable (x), you can combine them:
3x + 5x = 8x
- Solving Equations
An equation tells you that two things are equal. To solve an equation, you need to find the value of the variable that makes the equation true.
Example:
x + 6 = 10
Subtract 6 from both sides:
x = 4
Solving is about balancing both sides of the equation by doing the same operation to both.
- The Order of Operations
When solving algebraic expressions, use the order of operations (also known as PEMDAS):
P: Parentheses
E: Exponents
MD: Multiplication and Division (left to right)
AS: Addition and Subtraction (left to right)
Example:
Simplify 3 + 2 × (5 + 1)
First: (5 + 1) = 6
Then: 2 × 6 = 12
Finally: 3 + 12 = 15
- Using the Distributive Property
The distributive property helps when multiplying a number by a group of terms in parentheses.
Formula:
a(b + c) = ab + ac
Example:
3(x + 4) = 3x + 12
This rule makes it easier to expand and simplify expressions.
- Inequalities
Equations show that two expressions are equal. But sometimes, we deal with situations where one side is greater than or less than the other. These are called inequalities.
Symbols to know:
- < means less than
- > means greater than
- ≤ means less than or equal to
- ≥ means greater than or equal to
Example:
x + 3 > 5
Subtract 3 from both sides:
x > 2
This tells us that x can be any number greater than 2.
- Graphing on a Number Line
You can show solutions to equations and inequalities on a number line.
Example:
For x < 4, draw a circle at 4 (open circle because it’s not “equal to”) and shade everything to the left.
For x ≤ 4, use a filled-in circle and shade left.
Real-Life Applications of Algebra
Let’s look at a few everyday examples where algebra comes in handy:
Budgeting
You have $100 and spend x on a book. The rest is for lunch and snacks.
Equation: x + y = 100
Shopping Discounts
A $50 jacket is on sale for x% off.
Final Price: 50 – (x/100 × 50)
Travel
Distance = Speed × Time
If you travel at 60 km/h for x hours,
Distance = 60x
Common Mistakes in Algebra (And How to Avoid Them)
Even smart students make mistakes! Here are some common ones:
| Mistake | What to Remember |
| Forgetting to do the same operation on both sides of the equation | Always keep both sides balanced. |
| Combining unlike terms | Only like terms (same variable and exponent) can be added or subtracted. |
| Misusing the order of operations | Use PEMDAS correctly. |
| Dropping signs | Be careful with negative numbers and subtraction signs. |
| Thinking multiplication is commutative with variables and constants only | Remember: ab = ba, but a + b ≠ b + a in all cases. |
How to Practice Algebra
Learning algebra is like learning a sport or a musical instrument — practice is key. Here are tips to get better:
- Use worksheets and online tools (like Khan Academy, Mathway, or Study Rhino’s own practice section!).
- Work with friends or join a study group.
- Ask questions when you’re stuck. Understanding why something works is better than just memorizing.
- Use flashcards for key terms and formulas.
- Apply math in your daily life (budgeting, shopping, sports stats, etc.).
Fun Fact: Algebra Isn’t Just Numbers!
Did you know the word “algebra” comes from the Arabic word “al-jabr”, meaning “reunion of broken parts”? It was first used in a book written by a Persian mathematician named Al-Khwarizmi over 1000 years ago!
Today, algebra is a global language used in science, business, engineering, and even video game design.
Final Thoughts
Algebra doesn’t have to be scary or confusing. Once you understand its basic building blocks — variables, expressions, equations, and logical rules — you’ll find that algebra is just a smarter, more flexible version of the math you’ve always known.
At Study Rhino, we believe that learning should be engaging and accessible. Whether you’re a middle schooler just getting started or a high school student brushing up on your skills, mastering algebra opens up a whole new world of mathematical thinking.
Stay curious. Practice often. And remember — every equation has a solution!