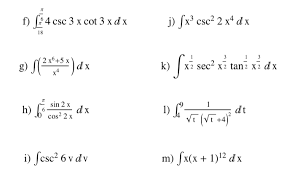How to Solve Calculus Problems

By Study Rhino

Calculus is one of the most powerful and widely used branches of mathematics. It helps us understand how things change and how to calculate areas, volumes, rates of change, and much more. Whether you’re a high school student, a college freshman, or preparing for competitive exams, mastering how to solve calculus problems is essential.

In this article, we’ll walk you through clear, step-by-step strategies to tackle calculus problems confidently. From understanding basic concepts to applying them in problem-solving, this guide covers it all.

What is Calculus?

Calculus is the mathematical study of change. It is divided into two main branches:

1. Differential Calculus – Focuses on the rate of change (derivatives).
2. Integral Calculus – Focuses on the accumulation of quantities (integrals).

Together, they form the backbone of many scientific fields like physics, engineering, economics, and even biology.

Step-by-Step Guide: How to Solve Calculus Problems

Step 1: Understand the Problem

Before rushing into calculations, pause and carefully read the problem. Ask yourself:

• What is being asked?
• Is it a rate of change (derivative) or total accumulation (integral)?
• Are there any functions, graphs, or equations involved?

Tip: Highlight keywords like “rate,” “area,” “instantaneous,” “maximum,” “minimum,” “increase,” or “decrease.” These often indicate whether to use differentiation or integration.

Step 2: Identify the Type of Problem

Different calculus problems require different approaches. Common types include:

• Finding the derivative of a function
• Finding the integral of a function
• Solving optimization problems
• Solving motion-related problems (position, velocity, acceleration)
• Area under curves
• Volume of solids of revolution
• Related rates problems
• Limits and continuity

Knowing the category helps you pick the right tool or formula.

Step 3: Recall the Relevant Formula or Rule

Here are some must-know calculus rules:

Derivatives:

• Power Rule:
  ddx(xn)=nxn−1\frac{d}{dx}(x^n) = nx^{n-1}dxd​(xn)=nxn−1
• Product Rule:
  ddx(uv)=u′v+uv′\frac{d}{dx}(uv) = u’v + uv’dxd​(uv)=u′v+uv′
• Quotient Rule:
  ddx(uv)=u′v−uv′v2\frac{d}{dx}\left(\frac{u}{v}\right) = \frac{u’v – uv’}{v^2}dxd​(vu​)=v2u′v−uv′​
• Chain Rule:
  ddx[f(g(x))]=f′(g(x))⋅g′(x)\frac{d}{dx}[f(g(x))] = f'(g(x)) \cdot g'(x)dxd​[f(g(x))]=f′(g(x))⋅g′(x)

Integrals:

• Basic Power Rule:
  ∫xndx=xn+1n+1+C\int x^n dx = \frac{x^{n+1}}{n+1} + C∫xndx=n+1xn+1​+C (for n≠−1n \neq -1n=−1)
• Integration by Substitution (Reverse of Chain Rule)
• Integration by Parts:
  ∫udv=uv−∫vdu\int u dv = uv – \int v du∫udv=uv−∫vdu

Step 4: Simplify the Expression First

Before applying a rule, always try to simplify the expression. Factor the function, cancel terms, or rewrite it in a form that’s easier to differentiate or integrate.

For example:

Instead of differentiating f(x)=x2+3xxf(x) = \frac{x^2 + 3x}{x}f(x)=xx2+3x​,
first simplify it to f(x)=x+3f(x) = x + 3f(x)=x+3.

Step 5: Apply the Appropriate Method

Now that you’ve identified the problem type and simplified it, use the correct method.

Let’s break it down further by example types.

Solving Derivative Problems

Example:

Find the derivative of f(x)=3×4−5×2+2f(x) = 3x^4 – 5x^2 + 2f(x)=3×4−5×2+2

Solution:

Use the power rule:

f′(x)=ddx(3×4)−ddx(5×2)+ddx(2)=12×3−10xf'(x) = \frac{d}{dx}(3x^4) – \frac{d}{dx}(5x^2) + \frac{d}{dx}(2) = 12x^3 – 10xf′(x)=dxd​(3×4)−dxd​(5×2)+dxd​(2)=12×3−10x

Solving Integral Problems

Example:

Find the integral of f(x)=4x3f(x) = 4x^3f(x)=4×3

Solution:

Use the power rule for integration:

∫4x3dx=4⋅x44+C=x4+C\int 4x^3 dx = 4 \cdot \frac{x^4}{4} + C = x^4 + C∫4x3dx=4⋅4×4​+C=x4+C

Optimization Problems

These problems ask for the maximum or minimum of a function, often in a real-world context.

Steps:

1. Find the derivative.
2. Set it to zero to find critical points.
3. Use a sign chart or second derivative test to determine maxima/minima.

Related Rates Problems

These problems involve finding the rate at which one quantity changes with respect to another.

Strategy:

1. Identify variables and their rates of change.
2. Use geometry or physics to relate variables.
3. Differentiate both sides with respect to time (t).
4. Substitute known values and solve.

Motion Problems

In physics, calculus is often used to analyze motion.

• Position: s(t)s(t)s(t)
• Velocity: v(t)=s′(t)v(t) = s'(t)v(t)=s′(t)
• Acceleration: a(t)=v′(t)=s′′(t)a(t) = v'(t) = s”(t)a(t)=v′(t)=s′′(t)

Example:

If s(t)=t3−6t2+9ts(t) = t^3 – 6t^2 + 9ts(t)=t3−6t2+9t, find the velocity at t=2t = 2t=2

Solution:

v(t)=ddt(s(t))=3t2−12t+9v(2)=3(4)−12(2)+9=12−24+9=−3v(t) = \frac{d}{dt}(s(t)) = 3t^2 – 12t + 9 \\ v(2) = 3(4) – 12(2) + 9 = 12 – 24 + 9 = -3v(t)=dtd​(s(t))=3t2−12t+9v(2)=3(4)−12(2)+9=12−24+9=−3

Area Under a Curve

To find the area between the graph of a function and the x-axis, use definite integrals.

Example:

Find the area under f(x)=x2f(x) = x^2f(x)=x2 from x=0x = 0x=0 to x=2x = 2x=2

∫02x2dx=[x33]02=83−0=83\int_0^2 x^2 dx = \left[ \frac{x^3}{3} \right]_0^2 = \frac{8}{3} – 0 = \frac{8}{3}∫02​x2dx=[3×3​]02​=38​−0=38​

Common Mistakes to Avoid

1. Forgetting Constants of Integration: Always add “+ C” for indefinite integrals.
2. Wrong Use of Product/Chain Rule: Make sure to apply all rules correctly, especially when functions are composed or multiplied.
3. Not Checking Domain: Some functions are not differentiable at certain points (like cusps or corners).
4. Ignoring Units: In applied problems, always include units in your final answer.

Tips to Improve Your Calculus Skills

1. Practice Consistently

The more you practice, the better you’ll understand patterns and problem-solving techniques. Use worksheets, online resources, or calculus apps.

2. Understand, Don’t Memorize

Instead of memorizing formulas blindly, try to understand why they work. For example, understand how the Chain Rule is derived and when to use it.

3. Visualize the Problem

Use graphs to understand the function’s behavior. Many calculus problems make more sense when you can see the curve.

4. Use Technology Wisely

Graphing calculators, Desmos, Wolfram Alpha, and other tools can help you check your answers or visualize graphs, but don’t rely on them to do all the thinking for you.

5. Study with Peers or Join a Forum

Collaborating with others can help you see problems from a different perspective and learn new techniques.

Real-Life Applications of Calculus

Knowing how to solve calculus problems isn’t just about passing exams. It’s used in:

• Physics: Motion, energy, and forces.
• Economics: Cost optimization, marginal analysis.
• Engineering: Design, signal processing, fluid dynamics.
• Biology: Population modeling, drug absorption rates.
• Computer Science: Machine learning algorithms, graphics, data analysis.

Summary: The Calculus Problem Solving Checklist

✅ Read and understand the problem
✅ Identify the type: derivative, integral, optimization, etc.
✅ Recall the correct rules/formulas
✅ Simplify the expression if possible
✅ Apply the method step-by-step
✅ Check your final answer (including units and domain)

Final Thoughts

Calculus doesn’t have to be intimidating. With the right mindset, clear strategies, and regular practice, you can become confident in solving calculus problems. Whether you’re studying for a test or just want to understand the math behind the world around you, remember that every complex problem starts with a single, simple step.

Keep learning, keep practicing, and trust the process—because at Study Rhino, we believe that every student can master calculus with the right support.