Geometry is one of the oldest and most fundamental branches of mathematics. It is all around us—in the shape of buildings, the design of everyday objects, the layout of cities, and even the structure of the universe. At its core, geometry is the study of shapes, sizes, angles, and dimensions.
If you’re new to geometry, understanding the key terms and definitions is the first step to mastering this subject. In this beginner-friendly guide, Study Rhino will walk you through the foundational concepts and vocabulary used in geometry. Whether you’re a student just starting out or someone looking for a refresher, this guide is your stepping stone to geometric success.
What Is Geometry?
Geometry comes from the Greek words geo (earth) and metron (measurement). Historically, it began as a practical way to measure land and spaces. Over time, it evolved into a rich field of mathematics that includes everything from simple shapes to complex three-dimensional structures and even abstract concepts like non-Euclidean geometry.
At the beginner level, we focus mostly on Euclidean geometry, which is the geometry taught in schools and is based on the work of the ancient Greek mathematician Euclid.
Basic Geometry Terms
Let’s begin by understanding some of the most fundamental terms in geometry:
- Point
- A point represents a location in space.
- It has no size, width, length, or depth.
- It is usually represented by a dot and named with a capital letter, e.g., Point A.
- Line
- A line is a straight, one-dimensional figure that extends infinitely in both directions.
- It has length but no width.
- A line is typically represented with two points on it and a double-headed arrow above them, e.g., ↔AB.
- Line Segment
- A line segment is part of a line that has two endpoints.
- It has a fixed length and does not go on forever.
- Written as AB (with no arrows).
- Ray
- A ray starts at one point and extends infinitely in one direction.
- It has a starting point but no end point.
- Denoted as →AB, where A is the starting point.
- Angle
- An angle is formed when two rays share a common endpoint.
- This common endpoint is called the vertex.
- The amount of turning between the two rays is measured in degrees (°).
- Angles can be named using three points, e.g., ∠ABC (B is the vertex).
Types of Angles
Understanding angles is essential in geometry. Here are the main types:
- Acute Angle – Less than 90°
- Right Angle – Exactly 90°
- Obtuse Angle – More than 90° but less than 180°
- Straight Angle – Exactly 180°
- Reflex Angle – More than 180° but less than 360°
- Full Rotation – Exactly 360°
Types of Lines
Different relationships between lines lead to important geometric concepts:
- Parallel Lines
- Lines that never intersect and are always the same distance apart.
- Denoted with the symbol ∥, e.g., AB ∥ CD.
- Perpendicular Lines
- Lines that intersect at a right angle (90°).
- Denoted with the symbol ⊥, e.g., AB ⊥ CD.
- Intersecting Lines
- Lines that cross at one point.
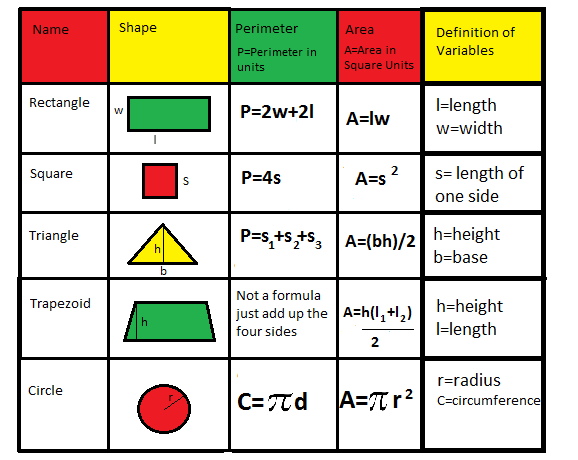
Basic Shapes and Figures
Geometry is filled with a variety of shapes. Here are the basic 2D shapes:
- Triangle
- A three-sided polygon.
- Sum of all interior angles is 180°.
- Types of triangles:
- Equilateral – all sides and angles are equal.
- Isosceles – two sides and two angles are equal.
- Scalene – all sides and angles are different.
- Right triangle – one angle is 90°.
- Quadrilateral
- A four-sided polygon.
- Includes:
- Square – four equal sides and all angles 90°.
- Rectangle – opposite sides equal, all angles 90°.
- Rhombus – all sides equal, opposite angles equal.
- Parallelogram – opposite sides parallel and equal.
- Trapezium – only one pair of opposite sides are parallel.
- Circle
- A round shape with no sides or corners.
- All points on the circle are equidistant from the center.
- Key terms:
- Radius – distance from center to edge.
- Diameter – longest distance across the circle, passing through the center (twice the radius).
- Circumference – the perimeter or distance around the circle.
- Chord – a line segment within the circle that does not pass through the center.
- Arc – a part of the circumference.
- Sector – a slice of the circle.
3D Geometry Terms
When shapes have depth in addition to length and width, they are 3-dimensional (3D).
- Solid Figures
Examples include:
- Cube – six equal square faces.
- Cuboid – like a box; faces are rectangles.
- Sphere – round object like a ball.
- Cylinder – two circular bases and one curved surface.
- Cone – one circular base and a pointed top.
- Pyramid – a polygon base with triangular sides that meet at a point.
- Face, Edge, Vertex
- Face – a flat surface on a 3D object.
- Edge – where two faces meet.
- Vertex (plural: vertices) – a corner where edges meet.
Measuring and Calculations
- Perimeter
- The distance around a 2D shape.
- For example, the perimeter of a rectangle = 2(length + width).
- Area
- The amount of surface a shape covers.
- Common formulas:
- Rectangle: Area = length × width
- Triangle: Area = ½ × base × height
- Circle: Area = π × radius²
- Volume
- The amount of space a 3D shape contains.
- Common formulas:
- Cube: Volume = side³
- Cuboid: Volume = length × width × height
- Cylinder: Volume = π × radius² × height
Key Definitions to Remember
Here’s a quick list of essential definitions for revision:
- Polygon: A closed figure with straight sides.
- Regular Polygon: All sides and angles are equal.
- Congruent Shapes: Same size and shape.
- Similar Shapes: Same shape, different size.
- Symmetry: A shape has symmetry if one half is a mirror image of the other.
- Transformation: Moving or changing a shape. Includes:
- Translation (slide),
- Rotation (turn),
- Reflection (flip),
- Dilation (resize).
Introduction to Coordinate Geometry
This branch of geometry uses a coordinate plane (x and y axes) to represent points and shapes.
- Coordinate Plane
- Formed by two number lines: the x-axis (horizontal) and y-axis (vertical).
- The point where they intersect is the origin (0, 0).
- Coordinates
- Every point is represented as (x, y).
- For example, (3, 2) means 3 units right and 2 units up from the origin.
Why Geometry Matters
Geometry is not just a school subject—it’s a life skill. It helps us:
- Understand the world spatially.
- Develop logical thinking and problem-solving abilities.
- Pursue careers in engineering, architecture, design, physics, and more.
Even in daily life, from arranging furniture to understanding maps, geometry is constantly in use.
Tips for Learning Geometry
- Practice drawing – Sketch figures and label key points.
- Use real-world examples – Identify shapes in your environment.
- Memorize formulas – Especially for area, perimeter, and volume.
- Solve problems regularly – Practice helps retain definitions and improve accuracy.
- Use tools – A ruler, compass, and protractor are essential for geometry work.
- Stay curious – Explore beyond the textbook. Geometry can be fun!
Final Thoughts
Geometry may seem abstract at first, but once you understand the basic terms and definitions, it becomes a fascinating and rewarding subject. Whether you’re identifying shapes in art, solving problems in math class, or planning a layout for your room, geometry gives you the tools to think spatially and logically.
At Study Rhino, we believe that strong foundational knowledge builds confident learners. Bookmark this guide, keep practicing, and soon you’ll be seeing geometry not just in your textbooks—but everywhere around you.